Ancora di probabilità e solitari
 Sta diventando una mania quella del calcolo probabilistico su giochi di carte, questa volta è toccato al solitario del prigioniero.
Sta diventando una mania quella del calcolo probabilistico su giochi di carte, questa volta è toccato al solitario del prigioniero.
Dato che il galeotto ha taaaaaanto tempo da far passare gli hanno inventato un passatempo talmente facile che anche una scimmia non ammaestrata lo saprebbe fare ma talmente difficile da far riuscire che… a voi capire il perché.
Le regole sono semplicissime: si mescola il mazzo e si estraggono le carte una a una, contando ogni carta estratta da 1 a 3, arrivati a 3 si rinizia da 1 fino alla fine del mazzo. Si perde tutte le volte che esce un asso all’1, un due al 2 ed un — provate a immaginare — tre al 3.
Se riuscite ad arrivare alla fine del mazzo dopo pochi tentativi vi potete considerare fortunati, visto che sulla solita simulazione da 1.000.000 partite appena 8200 sono vittoriose, che si traduce in uno 0,82% di riuscita.
Facendo il rapporto se volete avere qualche speranza di vincere questo gioco dovreste tentarlo almeno 120/130 volte, ma chissà, magari la dea bendata è dalla vostra parte e riuscite a farcela con meno.
Al solito aggiungo in calce l’applet java vergata dal sottoscritto per fare i test
No Java 2 SDK, Standard Edition v 1.4.1 support for APPLET!!

Veramente io ho eseguito il calcolo combinatorio abbastanza accuratamente e mi è venuto il numero 0.08307 % che differisce di un pochino dal 0.82 di cui sopra. Non so se Lei sia ancora interessato a questa cosa, comunque se vuole Le mando la formula. Cordiali saluti
Guido Fano
Dipartimento di Fisica
Università di Bologna
Ciao,
ti ringrazio per avermi inviato il tuo commento, certo che sono interessato 😀
Al tempo diedi l’esame di Calcolo di Probabilità e Statistica e chiesi alla prof. quale distribuzione utilizzare per calcolarne le probabilità, ma mi disse che non conoscendo il gioco non aveva idea (voglia?) di come risolverlo.
E’ per questo che, visto che non ci sono arrivato per formule, ho approfittato delle simulazioni al computer. La divergenza tra i risultati potrebbe essere imputabile in capo a 2 fattori:
1) L’approssimazione che uso per dicotomizzare tra le partite vinte e quelle perse (molto probabile);
2) Il generatore casuale che, essendo pseudo-randomico, diverge leggermente dal calcolo (plausibile ma meno probabile).
Se la formula si può scrivere nei commenti puoi rispondere al messaggio, al contrario puoi inviarmi un messaggio privato o per mail.
Ti faccio una domanda fuori tema: come hai raggiunto questo articolo? 🙂
Dunque, ho raggiunto questo articolo facendo su Google (ricerca avanzata) le parole “solitario carte probabilità” . Penso che la divergenza fra i due calcoli sia dovuta al fatto che i metodi “random” convergono lentamente, (se io non ho commesso errori il tuo metodo “converge in probabilità” al mio) quindi credo più all’opzione 2), anche perchè non ho capito cosa vuoi dire con “approssimazione che uso per dicotomizzare…” .
Piacerebbe anche a me, così per divertimento scrivere un programmino per eseguire il calcolo dicendo al computer di fare qualche milione di tentativi. Purtroppo non conosco Java ma solo il vecchio FORTRAN (ho 80 anni). Se mi dai il tuo indirizzo mail (il mio lo conosci) proverò a mandarti la formula. Ciao G.F.
Purtroppo il programma l’ho scritto ormai 2 anni fa e non ricordo bene tutti i passaggi dell’implementazione, non vorrei aver commesso qualche volgare errore sull’algoritmo pseudo-randomico o di controllo sulle vittorie (quello a cui facevo riferimento con la frase “approssimazione che uso per dicotomizzare…”).
Se la differenza è veramente di un’unità decimale (0.083% vs 0.82%) è interessante andare a rivedere il codice in cerca dell’errore o del perché di questa convergenza sospettosamente lenta.
Ad ogni modo la mia mail è:
saverio.giallorenzo AT gmail.com
attendo la formula e ancora grazie per l’interessamento 🙂
P.S. complimenti per l’età 😀 l’importante è tenere il cervello sempre in allenamento.
Nel caso fossi interessato a riprendere a programmare, ti consiglierei “ruby” o “python” che sono due linguaggi di scripting molto semplici da programmare ma comunque potenti e funzionali ai fini delle simulazioni (su cui si trovare un buon numero di pubblicazioni).
Caro Saverio,
Ti avevo chiesto l’indirizzo mail perchè pensavo di inviarti la formula scritta perbene in TEX , ma prima provo a vedere se posso scriverla qui, prevedo di avere qualche problema col simbolo “sommatoria”. Grazie per i complimenti e per il consiglio di usare “ruby”, ecc. , ma uno dei guai dell’età è che non si impara più un tubo, a meno di non fare una gran fatica.
Dunque, dividiamo le 40 carte in 3 insiemi, il primo A in cui dico “1” , il secondo B in cui dico “2” e il terzo C in cui dico “3”; le dimensioni di A,B,C, sono 14,13,13 rispettivamente perchè alla prima e l’ultima carta dico “1”.
Diciamo (N,M) il numero di modi di scegliere M oggetti fra N. La notazione matematica sarebbe il binomiale con N sopra e M sotto (per questo volevo usare il TEX) . Dunque
(N,M) = N.(N-1).(N-2)….(N-k+1) / ( 1. 2. 3…..k)
Devo disporre le carte che escono in modo che i quattro assi non cadano in A , i quattro 2 non cadano in B, e i quattro 3 non cadano in C. Diciamo ancora NB1, NC1 il numero di assi che cadono in B,C rispettivamente, NA2,NC2 il numero di 2 che cadono in A e C rispettivamente, e NA3, NB3 il numero di 3 che cadono in A e B . Ovviamente NB1+NC1=NA2+NC2=NA3+NB3= 4 .
Disponiamo i 2. Questo lo possiamo fare in (14,NA2) X (13,NC2 ) modi . Disponiamo ora gli assi. Poichè in C NC2 posti sono già occupati, possiamo farlo in (13,NB1)X(13-NC2,NC1) modi. Infine disponiamo i 3; questo possiamo farlo in (14+13-NA2-NB1, 4) modi possibili. Basta ora moltiplicare i binomiali e abbiamo i casi favorevoli, sommando ovviamente sui 25 casi ottenuti facendo variare NA2 da 0 a 4, ed NB1 da 0 a 4.
Quanto ai casi possibili, questi si ottengono scegliendo 12 posti su 40, in cui cadono gli assi, i 2 e i 3. Questo lo si può fare in (40, 12) modi; occorre poi moltiplicare per (12, 4) (8,4) che sono i modi di dividere le 12 carte in tre gruppi di 4 carte.
Ho evitato l’ostacolo di scrivere il simbolo di sommatoria; (ho detto “sommando ovviamente…” spero qualcosa si sia capito lo stesso.
Continuo a ritenere probabile che il tuo programma non era sbagliato. La convergenza dei metodi “tipo MonteCarlo” è sempre molto lenta. Magari proverò a scrivere un programmino così anch’io. Tu quante “prove” avevi usato? Dell’ordine del milione, immagino.
Ciao, Guido F.
Ho capito il ragionamento di fondo — decisamente più astuto del mio, che ho applicato le regola alla simulazione “bovinamente”, senza pensare alla divisione in gruppi.
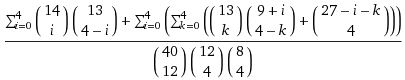
Penso di aver capito il ragionamento di fondo sulla divisione in tre gruppi e il calcolo delle combinazioni dei casi favorevoli, ecc.
Ho anche cercato di rifarmi i calcoli con wolfram alpha, ma per ora con scarsi risultati.
Chiedo conferma (o più probabilmente dis-conferma) della formula di seguito.
Intanto ne ho approfittato per rispolverare i vecchi appunti di CPS e ho attaccato il problema da un’altra prospettiva, pur continuando a considerare la divisione in gruppi. Ho calcolato la probabilità “semplice” di non estrarre nel gruppo A (quello degli “1”) degli assi, usando la distribuzione ipergeometrica.
In questo caso il calcolo mi ritorna il valore di 115/703 che è circa 16,3584%.
Già che c’ero ho calcolato anche quello di “2” e “3” come eventi indipendenti che è 135/703, circa 19,2034%
Poi pensavo di procedere con il calcolo delle probabilità condizionate, ma mi sono bloccato sul calcolo della probabilità dell’evento P(A unito B).
Non contento ho riscritto l’algoritmo della simulazione in ruby, giusto per vedere come poteva venire.
Lo copio/incollo di seguito:
cardBox=[] for i in 1..10 cardBox+=[i,i,i,i]; end lost=0 tries=10**8 a=0..13 b=14..26 c=27..39 start=Time.now tries.times{ |i| cardBox.shuffle! if cardBox[a].include?(1) lost+=1 elsif cardBox[b].include?(2) lost+=1 elsif cardBox[c].include?(3) lost+=1 end if i % (tries/10) == 0 puts "#{i*100/tries}%" end } finish=Time.now puts "Done in #{finish-start} seconds." puts "#{tries-lost}/#{tries}, #{(tries.to_f-lost)*100/tries}%"Con questo ho eseguito la simulazione su 10^8 iterazioni (c’è voluto un po’) ma ho ottenuto dei risultati interessanti.
L’algoritmo conferma il risultato (chiamiamolo intermedio) dato dalla distribuzione ipergeometrica sulla probabilità di non avere testa nel primo gruppo che è approssimato a 16,361024%.
Poi ho proceduto ad aggiungere il controllo sul secondo gruppo — P(A unito B) = 3,546697% — ed infine col terzo, che conferma il dato di 0,831378%.
A questo punto sono curioso di capire per bene la formula da te proposta per trovare la soluzione 🙂
Effettivamente c’è un errore nella tua formula: Tutti i binomiali sono corretti, ma li devi moltiplicare fra di loro prima di sommarli (parlo del numeratore, ovviamente), perchè ogni scelta di dove mettere il 2 va moltiplicata per tutte le scelte di dove mettere l’asso, ecc. Quindi avrai
“Sommatoria per i=0,1,2,3,4 ” X ” Sommatoria per k=0,1,2,3,4″ del prodotto di tutti i binomiali (14,i) (13,4-i) (13,k)(9+i,4-k) (27-i-k, 4). Il denominatore è corretto.
Se vuoi scrivere il programma, naturalmente devi costruirti prima una tabella di binomiali (triangolo di Tartaglia) usando la regola che un elemento è uguale alla somma dei due più vicini della riga precedente, regola che certamente saprai. Dico questo perchè non so se il computer vada in overflow a calcolare 27!, ecc. Fammi sapere se ottieni il mio 0.83070055% . Ciao
Mannaggia, mi sono reso conto dell’errore appena ho letto “devi moltiplicare” 🙂 Infatti non riuscivo a capire perché dovevano essere semplicemente sommati invece che moltiplicati e la risposta giusta era, ovviamente, la più ovvia.
Ad ogni modo ho riscritto la formula:
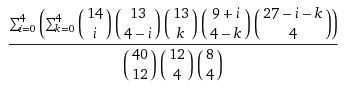
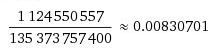
Il cui risultato è:
Quindi direi che, a meno di altri errori da parte mia, la soluzione matematica e quella ottenuta dalla simulazione convergono al secondo decimale, che non è un risultato eccelso, ma accettabile per “appena” 10^8 prove.
Ti ringrazio ancora per il tuo interessamento e per aver condiviso la soluzione 😀